En la primera parte, cuestionamos la forma habitual de evaluar el Error Absoluto Medio, que consiste simplemente en calcular la diferencia entre la media prevista y el resultado observado. Descubrimos que es necesario emplear el estimador puntual correcto, la mediana, para resumir la distribución en un solo número, de acuerdo con la interpretación operativa del Error Absoluto. Sin embargo, esto conlleva algunas propiedades bastante desagradables del MAE: es de grano grueso, discontinuo e inútil para elementos de movimiento lento.
Despeje el escenario para el Puntaje de Probabilidad Clasificada
Claramente, la situación con la que los dejé en la primera parte de esta publicación del blog no es satisfactoria: el MAE es discontinuo, impreciso e incluso inútil para los movimientos lentos con medias previstas inferiores a 0,69. No obstante, su interpretación empresarial razonable —el costo es proporcional al error— sigue siendo atractiva. ¿Podemos arreglarlo?
¿Podríamos simplemente descartar la mediana y usar algún otro método de resumen, como la media, mucho más benévola? Lamentablemente, pretender que la distinción entre mediana y media es irrelevante no la convierte en tal. Tomar ese camino no resuelve nuestros problemas, sino que introduce otros nuevos: la predicción que ganaría con un MAE evaluado incorrectamente estaría sesgada.
¿Cuáles son entonces nuestras posibilidades de mejorar la AE, dado que estamos limitados a la mediana como resumen? Hay un aspecto que podemos cambiar, a saber, el orden de los dos procesos “resumir” y “calcular el error”. Actualmente, primero resumimos (distribución mapeada a estimador puntual) y luego calculamos el error (“estimador puntual — resultado”). Respiremos hondo e intercambiemos los dos pasos, como se ilustra en el gráfico a continuación (lado izquierdo): Dada una distribución predicha (rojo) y un resultado observado (azul), calculemos el AE para cada resultado predicho (flechas negras):
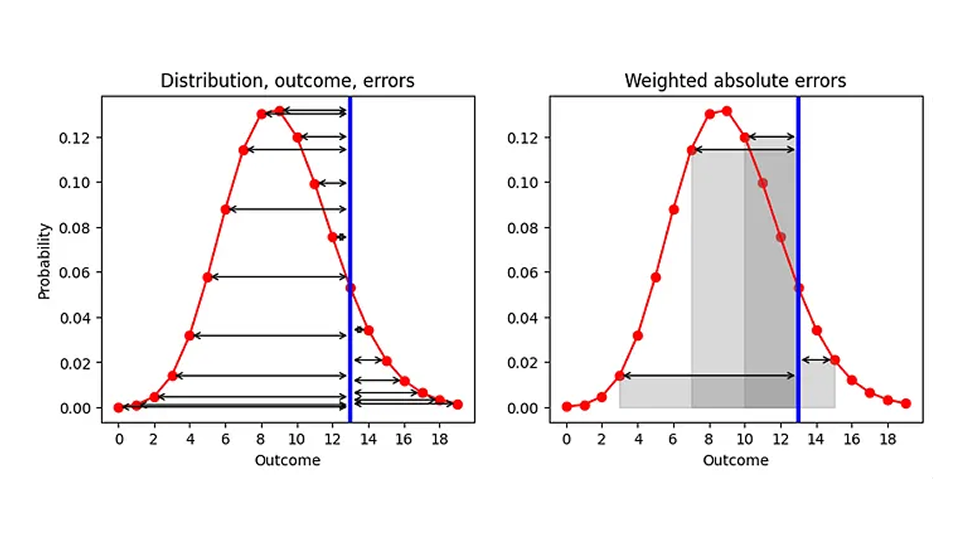
El resultado es una lista de AE, uno para cada resultado (incluido el de la predicción que coincide con el resultado real, para el cual AE es 0). Dado que nuestro objetivo es reemplazar AE por un número único, necesitamos resumir esos numerosos AE. Calculemos la media de los AE, ponderando dicha media con la probabilidad que asignamos a cada resultado. Geométricamente, estamos sumando las áreas encerradas por las flechas de error y el eje x, como se ilustra para algunos resultados en el gráfico de la derecha.
Esta prescripción constituye una definición razonable para la distancia entre un número y una distribución de probabilidad: se pondera cada distancia a un resultado posible según la probabilidad asignada a ese resultado. Como caso límite, si la distribución fuera 0 en todas partes excepto para un resultado, para el cual es 1 (un pronóstico determinista que predice que este resultado definitivamente se realizará), recuperamos el AE tradicional: El valor absoluto de la distancia entre ese resultado pronosticado determinísticamente y la observación. ¡Nuestro AE mejorado se convierte en el AE tradicional para pronósticos deterministas!
Podemos expresar la receta mediante esta fórmula:
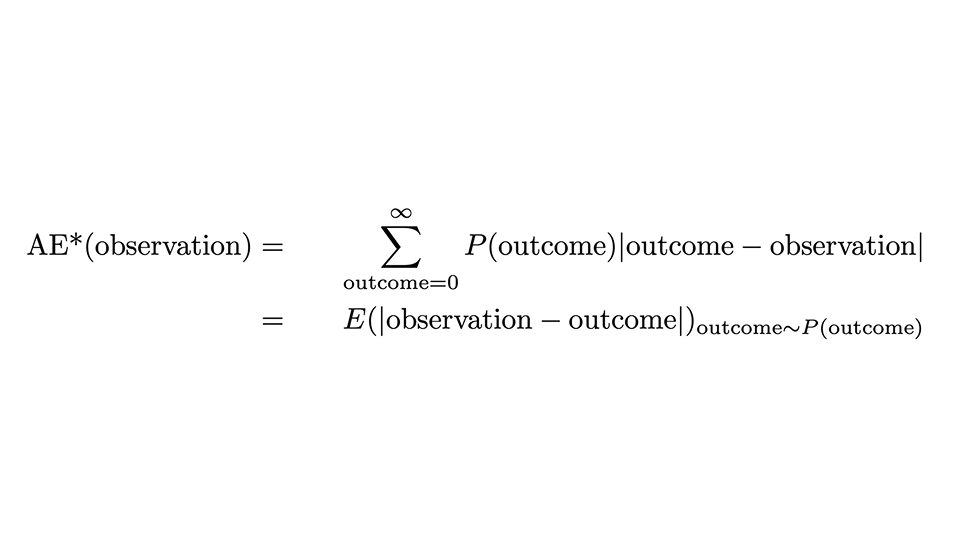
Parece un poco aterrador, pero vamos a analizarlo con calma: El AE*, el “AE corregido”, para una observación es el AE para esa única observación, pero promediado sobre todos los resultados posibles (la suma sobre el resultado), con la probabilidad predicha P(resultado) como ponderación. La segunda línea expresa que esto coincide con el valor esperado de la distancia absoluta entre la observación y el resultado, cuando el resultado se distribuye según la distribución de probabilidad.
¡Qué viaje! Todavía no llegamos, pero casi: el AE* no es exactamente el Puntaje de Probabilidad Clasificada, y todavía no tenemos ni idea de dónde proviene ese nombre tan engorroso.
El AE* definido anteriormente tiene una propiedad indeseable: cuando la distribución verdadera es una distribución de Poisson con un cierto valor medio, el AE* más bajo y mejor no se logra al hacer coincidir ese valor medio, sino uno ligeramente menor. Si tu pronóstico gana en AE*, probablemente esté sesgado y subestime la realidad. La razón es que el ancho absoluto de la distribución aumenta con el valor medio, lo que favorece valores medios más pequeños (una vez más, una oportunidad para promocionar las publicaciones anteriores del blog [enlaces a Forecasting Few is Different 1 y 2]). Este problema tiene solución: necesitamos restar la mitad del ancho esperado de la distribución para tener en cuenta eso, es decir, la distancia esperada entre dos resultados aleatorios tomados ambos de la distribución predicha. Finalmente, esto nos da la puntaje de probabilidad clasificada:
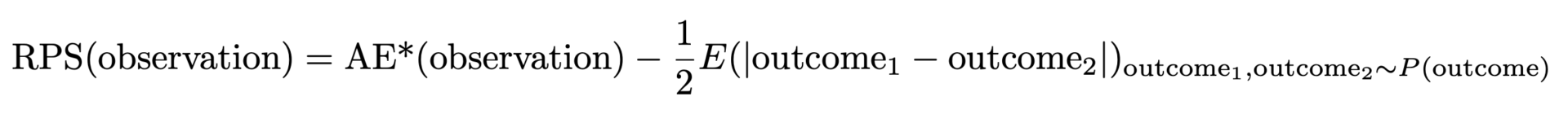
Pero, ¿por qué se llama Puntaje de Probabilidad Clasificada (RPS, por sus siglas en inglés) y por qué es tan impopular? El RPS se suele introducir mediante fórmulas abstractas que contienen numerosas probabilidades, funciones escalonadas y probabilidades acumulativas. A menudo se presenta con una interpretación puramente teórica de la probabilidad, lo cual tiene mucho sentido si uno está familiarizado con la teoría de la probabilidad y la estadística, pero que sigue siendo inaccesible para los profesionales. Es verdaderamente notable que las dos formulaciones —nuestra “AE mejorada” y la teórica de la probabilidad— coincidan: el patito feo (a ojos del profesional) se convierte en un hermoso cisne.
Cómo el puntaje de probabilidad clasificada resuelve las deficiencias del error absoluto medio
En la primera parte de esta publicación argumenté que el MAE tiene propiedades inconvenientes: es de grano grueso, discontinuo e inútil para elementos de movimiento lento. ¿Resuelve el RPS, el “MAE mejorado”, estos problemas? ¡Por supuesto que sí!
En el siguiente gráfico, se compara el RPS (línea negra) con el AE (línea azul), nuevamente para una observación de 9 (línea roja discontinua). Para predicciones que están lejos del resultado 9, RPS y AE se comportan de manera similar, y RPS simplemente se mantiene ligeramente por debajo de AE. Cuando la media prevista y la observada coinciden en 9, AE llega a cero, mientras que RPS es algo más escéptico: dado que RPS conoce la distribución, considera que acertar con la mediana de la distribución prevista también podría deber al azar: quizá la tasa de venta real ese día fue de 7, y simplemente tuvimos algo de suerte de que la demanda observada fuera de 9. Por lo tanto, RPS nunca llega a 0: ningún resultado individual demuestra inequívocamente que una predicción probabilística fue correcta. Al alejar del resultado 9, AE es estricto e inmediatamente penaliza “estar fuera de lugar” con el costo correspondiente. En este caso, RPS es más benevolente y no aumenta tan rápidamente como AE, lo que refleja que “estar un poco desviado” podría deber a la mala suerte y no necesita ser sancionado de inmediato. Esto se ajusta mucho mejor a la realidad empresarial: las operaciones a menudo se planean de manera que se toleren pequeñas desviaciones. Todo el mundo lo desea, pero nadie espera seriamente un pronóstico determinista, y existen reservaciones de seguridad para tener en cuenta esa posibilidad. Cuando las desviaciones son mayores, comienzan a generar costos reales.
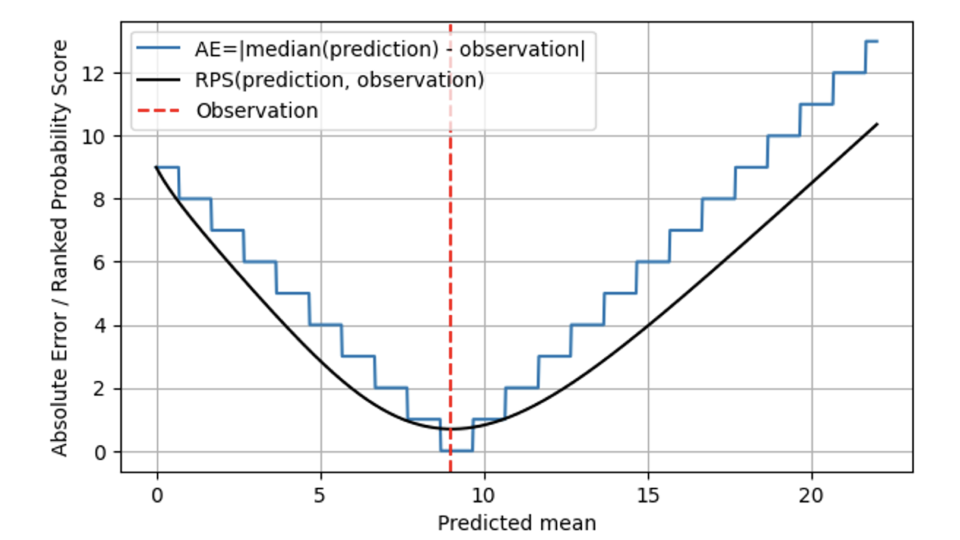
En general, el puntaje de probabilidad clasificada no “salta” entre diferentes valores, sino que, matemáticamente hablando, es continua en la media prevista. Para AE, las predicciones de 8,7, 9,3 y 9,6 son indistinguibles, para RPS sí se vuelven distinguibles: el RPS mínimo se alcanza exactamente en una media prevista de 9.
Para los productos de baja rotación, el RPS ayuda, pero no es una solución mágica: siempre será difícil distinguir un producto que se vende una vez cada 100 días de uno que se vende una vez cada 200 días, incluso si se emplea el RPS. Sin embargo, RPS asume valores diferentes incluso para predicciones pequeñas y diferentes como 0,6, 0,06 y 0,006.
RPS ayuda con muchos de los problemas de MAE, pero hay un desafío que ni siquiera RPS resuelve: el inevitable escalamiento que hace que los productos de venta lenta y rápida se comporten de manera diferente. Los métodos que hacen que las métricas sean conscientes de la escala (descritos en partes en este blog [enlaces a Forecasting Few is different 1 y 2]) pueden, sin embargo, aplicar a RPS de la misma manera que se aplicaron a AE. En comparación con el MAE relativo, el RPS medio relativo (el RPS medio dividido por la observación media) tiene una forma mucho más suave en este gráfico, lo que muestra el mejor valor alcanzable para ambas métricas:
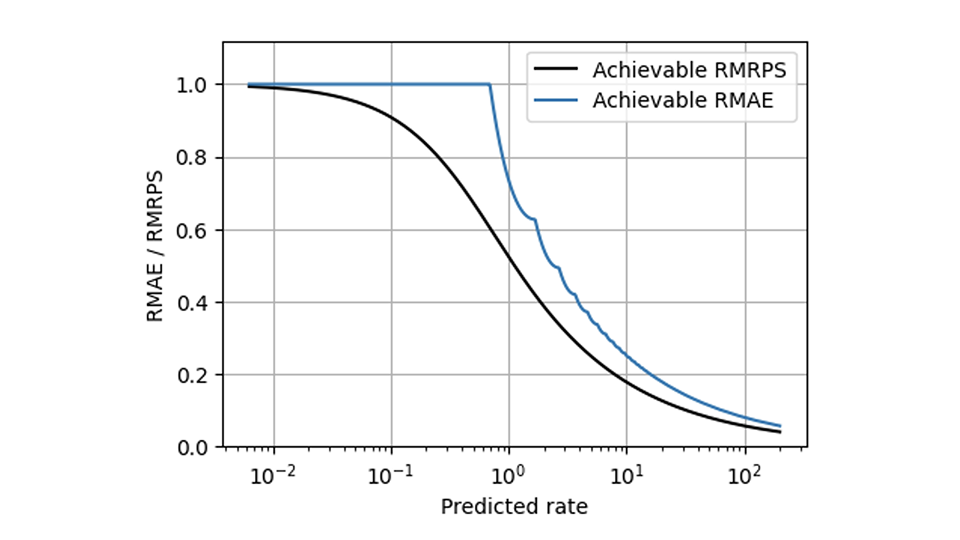
¿Cuándo se debe emplear MRPS en lugar de MAE?
Las predicciones significativas nunca son deterministas ni ciertas, sino probabilísticas e inciertas, lo cual debe tener en la evaluación. Decir que a los humanos no les gusta la incertidumbre es quedar corto: los humanos odian la incertidumbre. Las personas están dispuestas a poner en riesgo gran parte de la utilidad esperada para lograr una certeza perfecta (lo cual, cuando el riesgo es fatal, es algo razonable). Cuando a los interesados en el negocio se les dice que un pronóstico “solo” proporciona una predicción probabilística, a menudo prefieren una determinista, y los analistas deben decepcionarlos negar a elaborarla. Pero explicitar la incertidumbre inevitable no es un signo de debilidad, sino de confiabilidad.
Condensar toda la capacidad expresiva de una distribución de probabilidad, que contiene la probabilidad de cada resultado imaginable, en un solo número es tan simplista, burdo y tosco como parece; aunque esto es lo que hay que hacer operativamente cuando se almacenan artículos. Desde una perspectiva conceptual, el Puntaje de Probabilidad Ordenada ofrece, por lo tanto, una respuesta mucho mejor a la pregunta "¿cuán lejos está el resultado de la predicción?" que el Error Absoluto.
Siempre que la naturaleza probabilística del pronóstico sea irrelevante, la diferencia entre AE y RPS se vuelve insignificante y AE y RPS pueden usar indistintamente (el primero es más sencillo de calcular que el segundo, que asume valores ligeramente menores). Es decir, cuando la amplitud de la distribución de probabilidad es mucho menor que los errores típicos que se producen, yo, como pronosticador, no podré atribuir los errores que se producen a un “ruido inevitable contra el cual no se puede hacer nada”. Por ejemplo, cuando pronostico que ciertos artículos se venderán 1000 veces, y no soy particularmente ambicioso y ya estaría contento cuando los resultados estén en torno a 800 a 1200, la diferencia entre usar RPS y AE se vuelve marginal. Para simplificar, debería entonces atenerme a AE.
Siempre que nos encontramos en el régimen de movimiento medio a lento, es decir, cuando pronosticamos valores medios como 0,8, 7,2 o 16,8, marca la diferencia si condensamos la distribución en un solo número para evaluar AE o si optamos por el camino ligeramente más complejo empleando RPS. Cuando predecimos “1”, lo que queremos decir es que la probabilidad de observar “1” es de aproximadamente el 37%, y lo mismo ocurre con la probabilidad de observar 0. Por lo tanto, ignorar la naturaleza probabilística de los pronósticos en el régimen de ventas medio a lento es peligroso y engañoso. Pero ahora ya sabes cómo tener en cuenta la distribución de probabilidad: empleando el Puntaje de Probabilidad Ordenada, que espero que ahora también veas como el hermoso cisne de la evaluación de pronósticos, que logra satisfacer tanto a estadísticos como a profesionales.













