El error absoluto medio es la primera opción para los profesionales a la hora de evaluar sus modelos, debido a su definición simple y su relevancia intuitiva para el negocio. Por el contrario, la métrica de evaluación Ranked Probability Score no es una función realmente atractiva a primera vista: su nombre desalentador encaja bien con su engorrosa definición formal, lo que explica que casi ningún profesional de la cadena de suministro la conozca, y mucho menos la emplee. ¡Pero se lo están perdiendo! El puntaje de probabilidad clasificada es la extensión natural del error absoluto medio al ámbito de los pronósticos probabilísticos, es decir, a los pronósticos que “conocen” su propia incertidumbre. Incluye una interpretación intuitiva y resuelve varios de los problemas graves del Error Absoluto Medio. El puntaje de probabilidad clasificada refleja la realidad empresarial incluso mejor que el error absoluto medio, y tiene en cuenta la incertidumbre estadística, reconciliando así la teoría estadística académica con la práctica cotidiana.
Un estándar empresarial plausible: Error absoluto medio
¿Qué métrica debemos emplear para evaluar el modelo de previsión de la demanda?
Esa pregunta se suele responder con el “Error Absoluto Medio”, y con fundamentos bastante estables. El error absoluto (EA) a menudo refleja razonablemente el costo de que un pronóstico “sea erróneo”: cuando pronostico que se venderán 8 cestas de fresas, almaceno 8 cestas, pero la demanda real es de 9, tengo un EA de 1 y 1 cliente insatisfecho recurre a la competencia. Cuando mi pronóstico es de 11 cestas para la misma demanda de 9, el AE es 2 y tengo 2 cestas de fresas para desechar. Para ese resultado observado 9, el AE se muestra mediante la línea azul en el siguiente gráfico en función de la predicción:
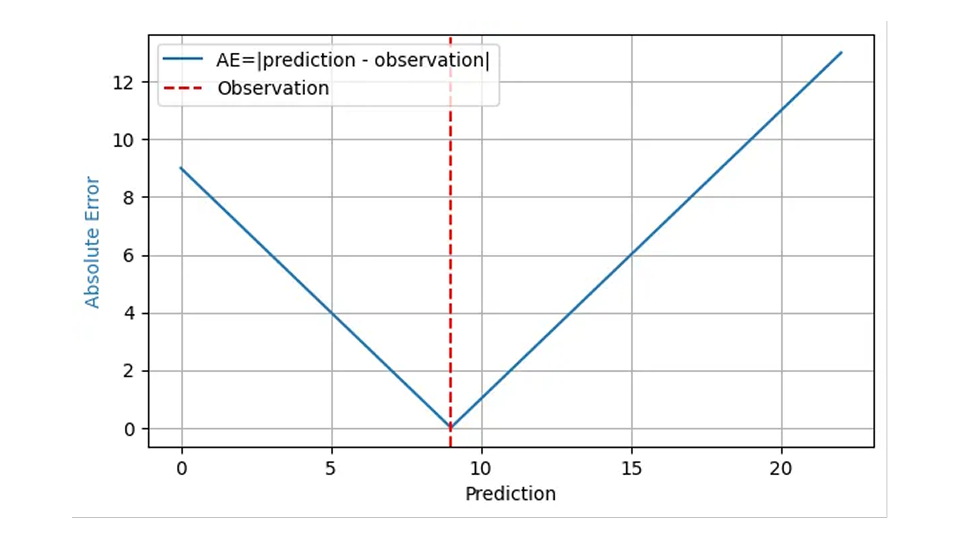
Dado que el impacto financiero de un error de pronóstico suele ser proporcional al propio error de pronóstico, la media del AE en muchas predicciones y resultados, el Error Absoluto Medio (MAE), refleja el costo empresarial, al menos bajo el supuesto de que un exceso de existencias tiene el mismo impacto financiero que una falta de existencias. El error cuadrático medio (MSE) indicaría que “desviar por una unidad” resulta más costoso cuanto mayor sea el error inicial, algo bastante irreal en los negocios. El error porcentual absoluto medio (MAPE), la media del AE estandarizado, Media (AE/resultado observado), sufre graves problemas inesperados (como se describe en esta publicación de blog anterior) y se puede descartar sin problemas para la previsión de la demanda.
Por lo tanto, se recomienda a los profesionales que empleen el MAE o su variante estandarizada, el MAE relativo (RMAE = MAE / Media(resultado)), como una primera opción sencilla para evaluar sus modelos. Sin embargo, los valores típicos de MAE y RMAE dependen de la escala: la previsión para botellas de leche (productos de venta rápida) tendrá, naturalmente, un MAE mayor y un RMAE menor que la previsión para algunas baterías especiales (productos de venta lenta). Hay que admitir que no es fácil de ver, por eso la contribución del blog dedicada a ese tema ni siquiera cabía en una sola publicación, sino que se dividió en "Pronosticar que pocos son diferentes, parte 1" y "parte 2".
Si MAE es simple, conocido y relevante, ¿por qué escribir o leer una entrada de blog sobre una alternativa? Pues bien, confiar ciegamente en una métrica de evaluación es sin duda una de las cosas menos científicas que se pueden hacer. Analicemos a fondo el MAE para ver si realmente se comporta como creemos que debería y, si no es así, cómo solucionarlo. En resumen: al evaluar los EA, encontrará algunas complicaciones inesperadas y desagradables, pero estas se resuelven fácilmente mediante una métrica relacionada pero bastante subestimada: la puntaje de probabilidad clasificada.
¡Espera, no tan rápido! Cómo evaluar el error absoluto medio para pronósticos probabilísticos
Hasta ahora, fingimos que “un pronóstico” es simplemente un número, al igual que el objetivo pronosticado (la cantidad de artículos vendidos, que podría ser la cantidad de cestas de fresas, manzanas, botellas de leche o camisetas rojas). Calcular la diferencia entre dicho pronóstico (un número) y la observación real (otro número) no supone ningún problema: predigo que se venderán 10 manzanas, se vendieron 7, el AE es 3. No se requiere doctorado en estadística.
Pero hay un matiz: ¿Qué pasó si predijo que se venderían 10,4 manzanas en lugar de 10? ¿Cuál fue mi decisión respecto al stock que debía mantener? Probablemente pidió igualmente 10 manzanas; es decir, la pequeña diferencia de 0,4 en la previsión no supuso ninguna diferencia operativa, el resultado comercial fue el mismo. Sin embargo, el error absoluto sería ligeramente mayor, 3,4 en lugar de 3. El comportamiento suave del error absoluto en la predicción de la primera figura es engañoso: la diferencia entre la predicción y el valor real no es la cantidad relevante para el negocio, sino la diferencia entre el número de artículos pedidos y el valor real. ¿Por qué habría de predecir algo que no fuera un número entero, si sé que solo pueden ocurrir cantidades enteras?
La razón de esta discrepancia —pronosticamos valores no enteros pero solo medimos cantidades enteras— es que la mayoría de los pronósticos no son “pronósticos puntuales” que expresen una “mejor estimación” universal e independiente de la evaluación para el objetivo, sino que proporcionan una distribución de probabilidad (no se preocupen: todavía no se necesita un doctorado en estadística). Nos dicen qué tan probable es cada resultado posible: al predecir 10,4, no pretendemos que algún cliente corte una manzana en pedazos para comprar 0,4 de una, pero consideramos que los resultados posibles “11”, “12”, “13” son más probables que para una predicción de 10,0. Por lo tanto, las previsiones no son solo números que se pueden comparar con el objetivo, sino funciones. Aunque la discusión se aplica a cualquier distribución, a lo largo de esta entrada de blog asumiré que la distribución de probabilidad prevista es la distribución de Poisson (consulte nuestras entradas de blog relacionadas aquí y aquí).
Aquí se muestra la distribución de probabilidad que asumimos implícitamente cuando predecimos 1,3, 3,8 o 11,7:
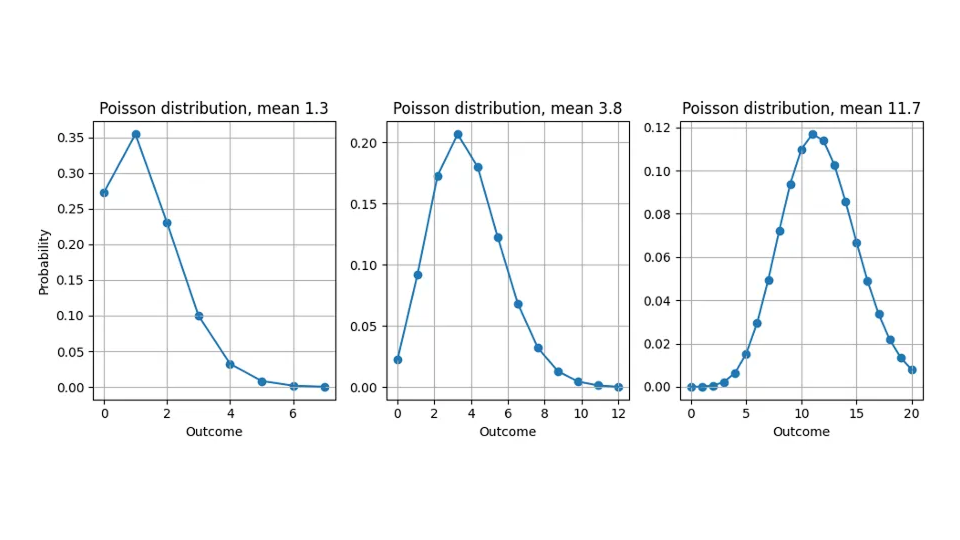
Volviendo a la evaluación del error absoluto: ¿Cómo podemos restar una función de un número? Restar 7 artículos vendidos de una distribución de probabilidad no tiene sentido. Necesitamos resumir la distribución de probabilidad prevista en un solo número para poder realizar una comparación. Este número resumen se denomina estimador puntual, que luego se puede restar del valor real observado para obtener el error.
Las distribuciones de probabilidad se pueden resumir de muchas maneras: la media es la más inmediata, pero las distribuciones también se pueden resumir por su resultado más probable (su moda), por el resultado que divide la distribución de probabilidad en dos mitades iguales (su mediana) o por otras prescripciones.
En ese zoológico de estimadores puntuales, algunos resultan más naturales que otros; ¿podemos simplemente elegir el resumen que más nos guste? No, el estimador puntual correcto viene determinado por la métrica de evaluación elegida. En otras palabras: Usted puede elegir qué métrica de error evalúa mi pronóstico (MAE, MAPE, MSE…), pero luego yo elijo cómo resumir el pronóstico para esa evaluación. Mi estimador puntual para ganar en MAE será diferente del que se usa para ganar en MSE, y ni hablar del MAPE. Esta elección puede parecerle arbitraria, incluso deshonesta, pero refleja el inmenso poder expresivo de las predicciones probabilísticas: contienen mucha más información que una simple “estimación”. Dependiendo de cómo se evalúen, de cómo se defina realmente "mejor" según la métrica de error, se elige el valor que resulta ganador para un método de evaluación determinado. En otras palabras: La pregunta “Dame tu mejor pronóstico” carece de sentido siempre y cuando no esté claro cómo se define “mejor”. Una única predicción probabilística puede producir muchos estimadores puntuales diferentes, o “mejores estimaciones”, dependiendo de cómo se evalúe la predicción.
Para el error cuadrático (SE), el estimador puntual es la media de la distribución. Para el Error Porcentual Absoluto (APE), el estimador puntual es una función realmente contraintuitiva con la que no me aburriré, lo que lleva a paradojas inesperadas en las evaluaciones de MAPE.
El error absoluto requiere la mediana de la distribución, no la media, y sí, eso importa.
Para el AE (Error Absoluto), el estimador puntual correcto resulta ser la mediana. Sí, la mediana, y no la media, y no, no podemos usar simplemente la media en su lugar. Permítanme explicarles por qué solo la mediana puede ser óptima para AE. Consideremos una previsión, es decir, una distribución, y digamos que es la distribución de Poisson con media 3,8 y mediana 4. ¿Cuántos artículos almacenas teniendo en cuenta esta previsión? El resultado es necesariamente un número entero, no puede ser 3.8. Para encontrar la cantidad correcta de acciones, elijamos la estimación tal que el AE que encontremos en promedio al observar los resultados de esa distribución sea lo más pequeño posible.
Buscamos el estimador puntual adecuado que condense toda esta distribución en un solo número, la mejor cantidad de existencias desde el punto de vista operativo. En esta figura, pruebo tres estimaciones diferentes (3, 4, 5):
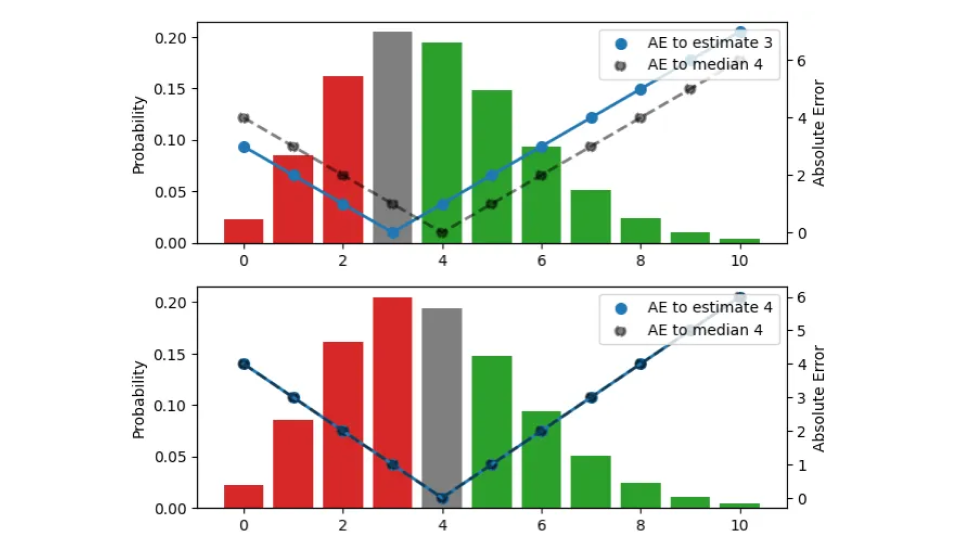

La distribución de probabilidad, visualizada mediante las barras (escala izquierda), es la misma en los tres paneles. El panel superior visualiza la estimación 3, en el panel central la estimación es 4, y en el panel inferior es 5. El AE entre la estimación y los resultados se muestra mediante los puntos azules, conectados por la línea continua (escala derecha), el AE con respecto a la mediana 4 se muestra mediante puntos negros, conectados por una línea discontinua. Por ejemplo, cuando la estimación es 3 (panel superior), el error para el resultado 3 desaparece y la línea azul continua llega a 0. Si la observación es 4 o 2, el error es 1.
El color de las barras indica si un resultado previsto contribuye al error absoluto porque es menor (rojo) o mayor (verde) que la estimación; la altura de la barra es la probabilidad de que ocurra. Cuando un resultado coincide con la estimación, su contribución al error es cero y se muestra en gris. Al desplazar la estimación una unidad hacia arriba , descendemos un panel, y todas las observaciones bajo las barras rojas y bajo la barra gris contribuyen con una unidad más de error a la nueva estimación desplazada: para la estimación anterior 3, el resultado 2 tenía un error de 1, pero para la estimación 4, el mismo resultado tiene un error de 2. Por otro lado, todas las observaciones que tenían barras verdes ahora contribuyen con una unidad menos de error tras el desplazamiento: para la estimación 3, el resultado 5 tenía un error de 2, para la estimación 4, el error disminuye a 1.
Resumamos lo que sucede cuando la estimación aumenta en una unidad: El valor esperado de AE bajo la distribución aumenta para aquellos resultados que son menores o iguales a la estimación (los sobreestimamos aún más de lo que lo hicimos) y disminuye para aquellos que son mayores que la estimación (los subestimamos menos). El aumento es proporcional al área total de las barras rojas y grises, la disminución es proporcional al área de las barras verdes.
De manera totalmente análoga, al disminuir la estimación en una unidad, las observaciones bajo las barras verdes o bajo la barra gris contribuyen a una unidad más de error cada una, y todas las observaciones en las barras rojas contribuyen a una unidad menos de error.
Para una distribución dada, desplazar la estimación hacia arriba o hacia abajo en una unidad aumenta o disminuye el error absoluto esperado resultante, y podemos buscar la estimación puntual correcta buscando el mínimo. Es posible que ya ideaste esta regla general: si, para la estimación actual, la mayoría de los resultados son subestimaciones, disminuye la estimación; si la mayoría de los resultados son sobreestimaciones, auméntala. Solo cuando la diferencia entre las masas de probabilidad relacionadas con las sobreestimaciones y subestimaciones (la diferencia entre las áreas totales de las barras “rojas” y “verdes”) es menor que la barra gris, no se puede mejorar más el error. Este es el caso en el panel central: la estimación es tal que las masas de probabilidad por debajo y por encima de ella casi coinciden, de modo que mover en cualquier dirección aumentaría el error total. Esta estimación coincide con la mediana: cuando se le da una distribución de probabilidad, el estimador puntual que minimiza el error absoluto será mayor o menor que los resultados en la mitad de los casos.
Creo que vale la pena recalcar este punto, porque a menudo se pasa por alto: cuando 7,3 es la mejor estimación para la media de una distribución, la forma correcta de evaluar el error absoluto con respecto a una observación de, digamos, 9, no es restar 7,3 de 9, sino restar la mediana de esa distribución (que es 7 para la distribución de Poisson) de 9. Operativamente, 7 es precisamente el número de artículos que se almacenarían, dada una predicción de 7,3. Sorprendentemente, no ayuda tener una estimación precisa del valor medio para las decisiones bursátiles, da igual que la previsión sea de 7,1 o de 7,3: Debes elegir un número entero. Sin embargo, al agregar pronósticos a un nivel superior para la planeación, la distinción entre 7.1 y 7.3 se vuelve importante.
Esta distinción entre media y mediana puede parecerle una cuestión de matices: luego de todo, el valor que divide la probabilidad en dos mitades iguales y la media de esa distribución parecen muy similares, y son cercanos para la mayoría de las distribuciones benévolas (como la distribución de Poisson que es pertinente para el comercio minorista). Sin embargo, dos distribuciones pueden tener la misma media, pero diferentes medianas; otras dos distribuciones podrían coincidir en la mediana pero diferir en su media. Emplear la media y la mediana como sinónimos impediría encontrar realmente la mejor previsión.
Las deficiencias inesperadas del error absoluto medio
Ahora sabemos cómo evaluar el error absoluto para pronósticos probabilísticos: resumimos la distribución mediante la mediana del estimador puntual (la cantidad de artículos que almacenaríamos), restamos esa mediana del resultado observado y tomamos el valor absoluto. Intenté visualizar esto en el siguiente gráfico:
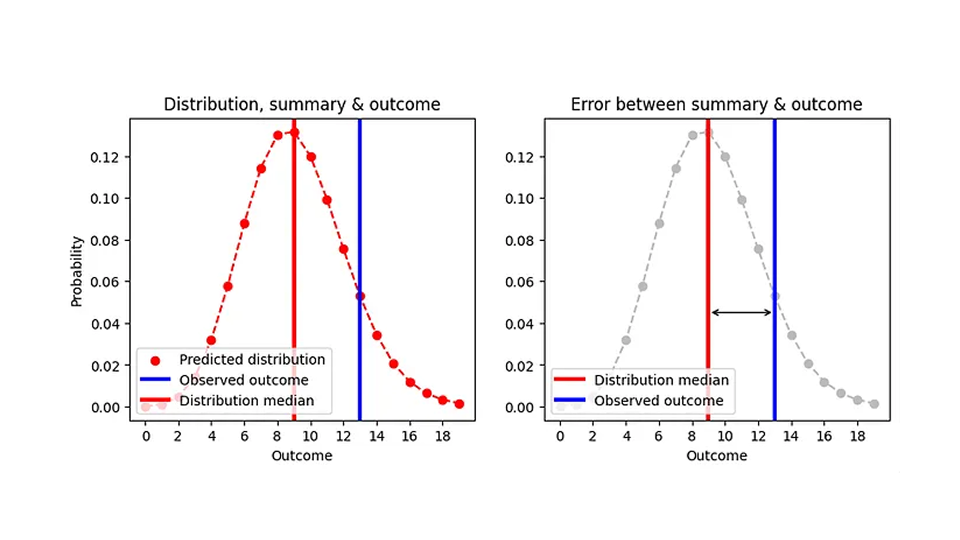
Dado que la mediana siempre es un número entero, dos distribuciones bastante diferentes pueden producir el mismo error absoluto. Por ejemplo, el AE para un pronóstico de Poisson de 8,7 (mediana=9) y para un pronóstico de Poisson de 9,6 (mediana=9) es el mismo, aunque los pronósticos son claramente diferentes, como podemos ver en esta figura:
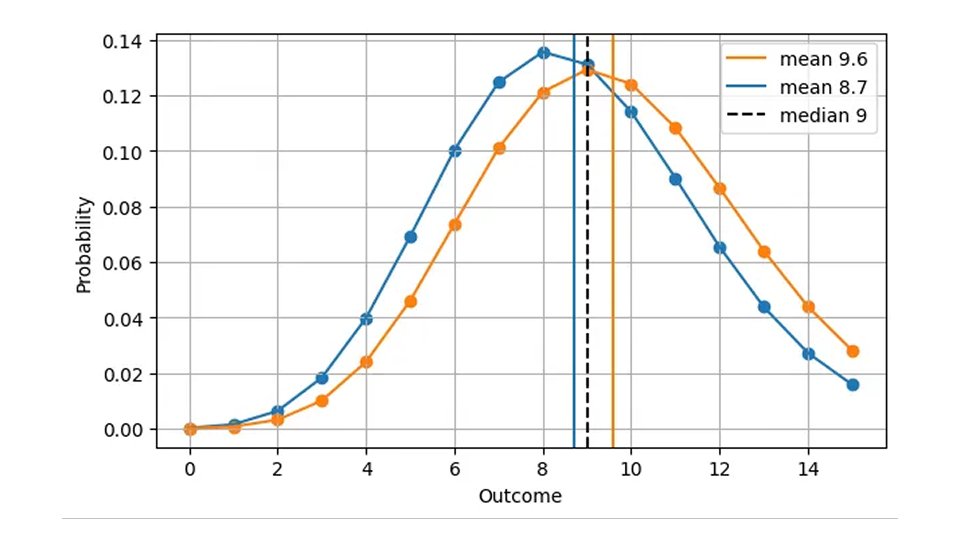
Esto tiene sentido desde el punto de vista operativo: en ambos casos, lo correcto es tener 9 artículos en stock en un día determinado. En consecuencia, una versión más realista de la primera figura, AE en función de la predicción, es la siguiente.
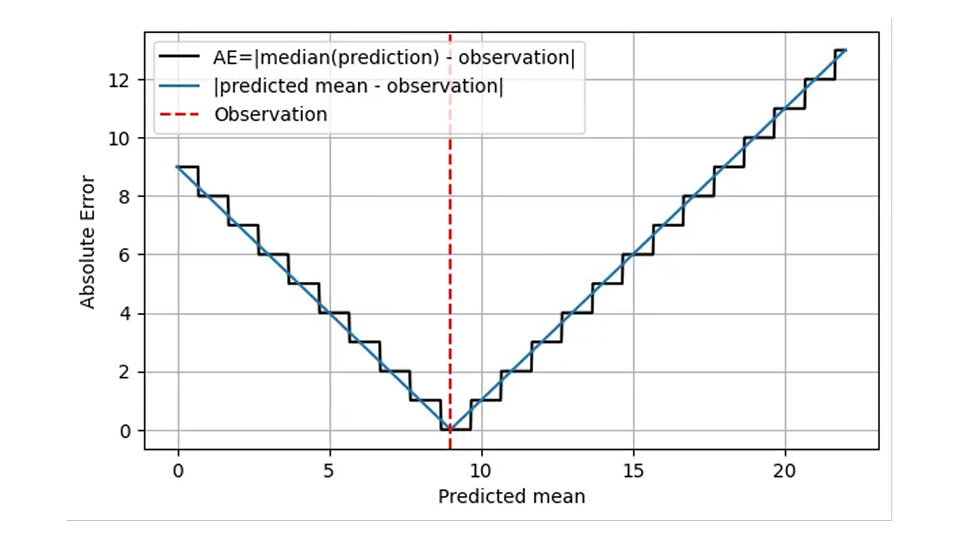
El AE se calcula empleando la mediana de la predicción (línea negra) y solo asume valores enteros. Voy a ser un poco más específico sobre lo que significa el eje x: no es solo “predicción”, sino la media prevista.
Esta forma escalonada implica que AE es de grano grueso e impreciso: ¡Podemos, a simple vista, distinguir las distribuciones con media 8,7 y 9,6, pero AE no puede! El MAE por sí solo no te ayudará a mejorar la precisión de un pronóstico más allá de cierto umbral, que es bastante sustancial para elementos de movimiento lento: la diferencia relativa entre 1,7 y 2,6 asciende al 53%, mientras que el AE de un pronóstico de 1,7 y el de un pronóstico de 2,6 son iguales. Ese comportamiento de grano grueso viene acompañado de saltos bruscos, discontinuidades en los valores en los que la mediana de la distribución salta de un valor entero al siguiente. Operativamente, no hay diferencia en predecir 1,7 o 2,6 para un día, ubicación y artículo determinados: la cantidad correcta para almacenar es 2. Sin embargo, los pronósticos también se emplean en niveles de agregación más altos para la planeación. En ese nivel tan alto, uno sí nota la diferencia entre 1,7 y 2,6: durante los próximos 100 días, supone una gran diferencia si se piden 170 o 260 artículos al proveedor.
Cuando la media prevista es inferior a aproximadamente 0,69 por periodo de tiempo de predicción (un vendedor lento), la predicción que le da el mejor error absoluto es 0. De manera bastante dramática, tenemos el mismo error absoluto para un pronóstico de 0,6, de 0,06 y de 0,006, ¡incluso cuando pasamos por dos órdenes de magnitud! La predicción 0 es bastante inútil en la cadena de suministro, ya que se entra en el círculo vicioso de pronósticos perfectos de 0: se almacena 0, se vende 0 y el pronóstico anterior de 0 se cumplió por sí mismo.













