El sesgo de selección retrospectivo surge cuando las predicciones de pronóstico probabilísticas y los datos reales observados no se agrupan adecuadamente al evaluar la precisión del pronóstico en diferentes frecuencias de ventas. Por un lado, el sesgo de selección retrospectivo es una trampa insidiosa que te lleva a conclusiones erróneas sobre el sesgo de un pronóstico probabilístico determinado; en el peor de los casos, te permite elegir un modelo peor en lugar de uno mejor. Por otro lado, su resolución y explicación tocan fundamentos estadísticos como la representatividad de la muestra, la predicción probabilística, las probabilidades condicionales, la regresión a la media y la regla de Bayes. Además, nos hace reflexionar sobre lo que intuitivamente esperamos de un pronóstico y por qué eso no siempre es razonable.
Los pronósticos pueden referir a categorías específicas : ¿habrá tormenta eléctrica mañana? —o cantidades continuas— ¿cuál será la temperatura máxima mañana? Aquí nos centramos en un caso híbrido: cantidades discretas, que podrían ser, por ejemplo, el número de camisetas que se venden en un día determinado. Dicha cifra de ventas es discreta, podría ser 0, 1, 2, 13 o 56; pero ciertamente no -8,5 o 3,4. Nuestro pronóstico es probabilístico; no pretendemos saber con exactitud cuántas camisetas se venderán. Un enfoque realista, aunque ambiciosamente limitado (es decir, La distribución de probabilidad precisa es la distribución de Poisson. Por lo tanto, asumimos que nuestro pronóstico produce la tasa de Poisson que creemos que impulsa el proceso de ventas real.
¿Un pronóstico bastante mediocre?
Supongamos que se emitió el pronóstico, se recopilaron las ventas reales y el pronóstico se evalúa mediante la siguiente tabla:
| Frecuencia de ventas observada | ventas medias observadas | Predicción media |
| Lento 0, 1, 2 piezas/día | 0.804 | 1.373 |
| Medio 3-10 piezas/día | 5.119 | 4.601 |
| Rápido >10 piezas/día | 13.880 | 11.041 |
Los datos se agrupan según la frecuencia de ventas observada: agrupamos todos los días en grupos en los que la camiseta se vendió pocas (0, 1 o 2), intermedia (de 3 a 10) veces o muchas (más de 10) veces. A primera vista, esta tabla grita inequívocamente: “Los productos de baja rotación están sobreestimados, mientras que los de alta rotación están subestimados”. El pronóstico es tan obviamente erróneo que inmediatamente nos apresuraríamos a corregirlo, ¿o no?
En realidad, y quizás sorprendentemente, todo está bien. Sí, es cierto que las ventas de los productos que se venden lentamente están sobreestimadas y las de los que se venden rápidamente están subestimadas, pero la previsión se comporta tal como debería. Es nuestra expectativa —que las columnas “ventas medias observadas” y “predicción media” deberían ser iguales— la que resulta errónea. Estamos ante un problema psicológico, con nuestras expectativas poco realistas, ¡y no ante un mal pronóstico! Un pronóstico probabilístico nunca prometió ni podrá jamás garantizar que, para cada grupo posible de resultados, el pronóstico promedio coincida con el resultado promedio.
Exploremos por qué ocurre esto, cómo resolver este dilema de manera satisfactoria y cómo evitar sesgos similares.
¿Qué es lo que realmente pedimos?
Retrocedamos un paso y expresemos con palabras lo que revela la tabla. Los datos se agrupan empleando las ventas observadas realmente; es decir, filtramos o condicionamos las predicciones y las observaciones según si estas últimas se encuentran dentro de un rango determinado (ventas lentas, medias o rápidas). La primera fila contiene todos los días en los que la camiseta se vendió 0, 1 o 2 veces; su columna central nos proporciona:

es decir, la media de las observaciones en el grupo en el que agrupamos todas las observaciones que son 2, 1 o 0; definitivamente un número entre 0 y 2, que resulta ser 0,804. La columna de la derecha contiene la predicción media esperada para el mismo grupo de observaciones.

Es decir, para todas las observaciones que sean 2 o menos, tomamos la predicción correspondiente y calculamos la media de todas estas predicciones.
A priori, no hay razón para que la primera y la segunda expresión tengan el mismo valor, pero intuitivamente nos gustaría que lo tuvieran: esperar que la predicción media sea igual a la observación media no parece pedir demasiado, ¿verdad?
| Frecuencia de ventas observada | ventas medias observadas | Predicción media |
| Lento 0, 1, 2 piezas/día | E (observación | observación ≤ 2) | E (predicción | observación ≤ 2) |
| Medio 3-10 piezas/día | E (observación | observación ≤ 3, ≤ 10 ) | E (predicción | observación ≤ 3, ≤ 10] ) |
| Rápido >10 piezas/día | E (observación | observación ≥ 11) | E (predicción | observación ≥ 11]) |
Previsión prospectiva, retrospectiva
En consonancia con su etimología, las predicciones son prospectivas y nos proporcionan las probabilidades de observar resultados futuros.
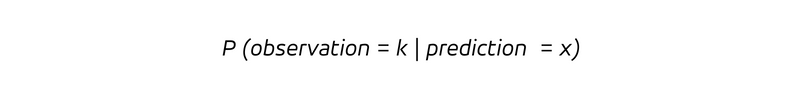
que es la probabilidad condicional de observar un resultado k, dado que la tasa prevista es x. Dado que tenemos una probabilidad condicional , consideramos la distribución de probabilidad para las observaciones asumiendo que la predicción tomó el valor x. Para una predicción imparcial, el valor esperado de la observación condicionado a una predicción x, es decir, la observación media bajo el supuesto de una predicción de valor x, es:
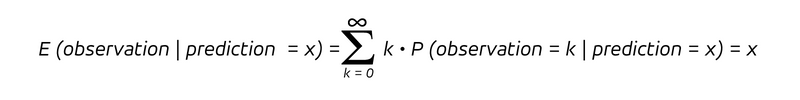
Eso es lo que promete cualquier pronóstico imparcial: agrupando todas las predicciones del mismo valor x, la media de las observaciones resultantes debería aproximar a ese mismo valor x. Si bien la distribución podría adoptar muchas formas diferentes, esta propiedad es esencial.
Volvamos a observar la tabla: lo que hacemos en la columna izquierda no es agrupar/condicionar por predicción, sino por resultado. La columna de la derecha, por lo tanto, pregunta retrospectivamente “¿cuál fue nuestra predicción media, dado un cierto resultado k?” en lugar de prospectivamente “¿cuál será el resultado medio, dada nuestra predicción x?”.
Para expresar la declaración retrospectiva en términos de la prospectiva, aplicamos la regla de Bayes.

Las preguntas retrospectivas y prospectivas son diferentes, y también lo son sus respuestas: aparecen otros términos, P (predicción = x) y P (observación = k), las probabilidades incondicionales de una predicción y un resultado. En consecuencia, el valor esperado de la predicción media, dado un resultado determinado, se convierte en:

Ejemplo minimalista
¿Qué valor asume E (predicción | observación = m) ? ¿Por qué no se simplificaría simplemente a la observación m?
En la gran mayoría de los casos, se cumple que E (predicción | observación = m) ≠ m. ¡Veamos por qué!
Consideremos una camiseta que se vende igual de bien todos los días, siguiendo una distribución de Poisson con tasa 5. La misma tasa prevista, 5, se aplica para todos los días. El resultado, sin embargo, varía. Claramente, 5 es una sobreestimación para los resultados de 4 y menores, y una subestimación para los resultados de 6 y mayores. Si volvemos a agrupar por resultados, nos encontramos con:
| Frecuencia de ventas observada | ventas medias observadas | Predicción media |
| Lento <5 piezas/día | 3.0082 | 5 |
| Medio 5 piezas/día | 5 | 5 |
| Rápido >5 piezas/día | 7.2844 | 5 |
De nuevo, a partir de esta tabla concluimos que los días de ventas lentas se sobreestimaron y los días de ventas rápidas se subestimaron, y así fue. Se cumple para cada observación E (predicción | observación = m) = 5, ya que la predicción siempre es 5.
El pronóstico sigue siendo “perfecto”: los resultados se comportan exactamente como se predijo, siguen la distribución de Poisson con tasa 5. La impresión de subestimación y sobreestimación de los pronósticos es puramente el resultado de la selección de datos: al seleccionar los resultados superiores a 5, conservamos aquellos resultados que están por encima de la predicción 5 y que fueron subestimados; al seleccionar los resultados inferiores a 5, conservamos los eventos inferiores a la predicción 5, que fueron sobreestimados. En una previsión probabilística, es inevitable que algunos resultados se hayan subestimado y otros se hayan sobreestimado. Al esperar que el pronóstico sea imparcial, esperamos que la subestimación y la sobreestimación se equilibren para una predicción m dada. Lo que no podemos esperar es que, al seleccionar activamente las observaciones sobreestimadas o subestimadas, estas no resulten estar sobreestimadas o subestimadas, respectivamente.
En una situación realista, no nos encontraremos con una previsión que asuma el mismo valor para cada día, sino que la predicción en sí variará. Sin embargo, seleccionar resultados “bastante grandes” o “bastante pequeños” equivale a mantener los eventos subestimados o sobreestimados en las categorías. Por lo tanto, en general tenemos que E (predicción | observación = m) ≠ m . Más precisamente, cuando m es tan grande que seleccionarlo equivale a seleccionar eventos subestimados, tendremos E (predicción | observación = m) < m; cuando m es suficientemente pequeño como para que seleccionarlo equivale a seleccionar eventos sobreestimados, E (predicción | observación = m) > m.
Predicciones deterministas: ¡siempre debiste haberlo sabido!
¿Por qué nos resulta esto desconcertante? ¿Por qué nos incomoda esa discrepancia entre la observación media y la previsión media? Nuestra intuición se basa en la igualdad entre predicción y observación que caracteriza los pronósticos deterministas . En términos de probabilidades, una predicción determinista se expresa como: P (observación = predicción) = 1 y P (observación ≠ predicción) = 0
La analista cree que la observación coincidirá exactamente con su predicción, es decir, los valores predichos y observados coinciden con una probabilidad de 1 (o 100%), mientras que todos los demás resultados se consideran imposibles. Es una afirmación segura de sí misma, por no decir audaz. Expresado mediante probabilidades condicionales, podemos resumir:

En otras palabras, siempre que predigamos vender k piezas (la condición luego de la barra vertical), venderemos k piezas. Dado que el determinismo no solo implica que cada vez que predecimos k observamos k, sino también que cada observación k fue predicha correctamente ex ante como k, tenemos:
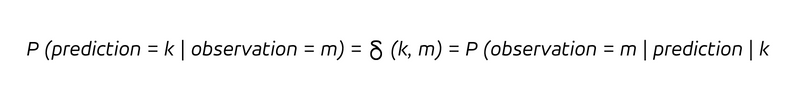
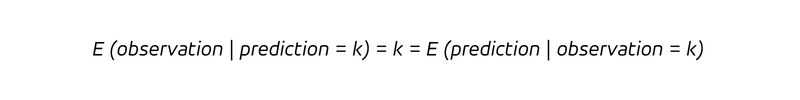
El determinismo hace obsoleta la distinción entre preguntas retrospectivas y prospectivas. Con una predicción determinista, no aprendemos nada nuevo al observar el resultado (¡ya lo sabíamos!), y no actualizaríamos nuestra creencia (que ya era correcta).
En un pronóstico tan determinista, en el que todas las distribuciones de probabilidad aparentes convergen a un máximo del 100% en el único resultado posible, no se produce ningún sesgo de selección retrospectivo: pretendemos haberlo sabido con exactitud de antemano, por lo que deberíamos haberlo sabido, siempre y bajo cualquier circunstancia. Si la medición indica lo contrario, su pronóstico “determinista” es erróneo.
Toda predicción seria es probabilística.
Las predicciones probabilísticas hacen afirmaciones más débiles que las deterministas, y para las predicciones probabilísticas debemos abandonar la idea de que cada resultado m se predijo que sería m en promedio; por lo tanto, las predicciones deterministas parecen muy atractivas. Pero, ¿es realista predecir de forma determinista las ventas diarias de camisetas? Supongamos que pudiste hacerlo y predijimos que las ventas de camisetas de mañana serán de 5. Eso significa que puedes nombrar a cinco personas que, pase lo que pase (accidente, enfermedad, tormenta, cambio repentino de opinión…), comprarán una camiseta roja mañana. ¿Cómo podemos esperar alcanzar tal nivel de certeza? ¿Alguna vez estuviste tan seguro de que comprarías una camiseta roja al día siguiente? Incluso si cinco colegas prometieran comprar una camiseta mañana bajo cualquier circunstancia, ¿cómo podrías descartar que alguien más, entre todos los demás clientes potenciales, también comprara una camiseta? Salvo ciertos casos extremos muy idiosincrásicos (muy pocos clientes, nivel de existencias mucho menor que la demanda real), predecir de forma determinista el número exacto de ventas de un artículo es imposible. La incertidumbre solo puede controlar hasta cierto punto, y cualquier pronóstico realista es probabilístico.
Evaluación de la higiene
Existe una forma alternativa de refutar la tabla 1: al configurar la tabla, planteamos una pregunta estadística, a saber, si el pronóstico está sesgado o no, y en qué dirección (ignoremos por el momento la cuestión de la significación estadística y supongamos que cada señal que vemos es estadísticamente significativa). Al igual que cualquier análisis estadístico, un análisis de pronóstico puede sufrir sesgos. La forma en que seleccionamos los resultados es un claro ejemplo de sesgo de selección: los eventos en los grupos “vendedores lentos”, “vendedores medios” y “vendedores rápidos” no son representativos del conjunto completo de predicciones y observaciones, pero los agrupamos en aquellos subestimados y sobreestimados. Además, empleamos lo que se denomina “información futura” en la evaluación de las previsiones: las categorías en las que agrupamos las predicciones y las observaciones no están definidas en el momento de la predicción, sino que se establecen a posteriori. Por lo tanto, la forma en que configuramos la tabla viola los principios básicos de los análisis estadísticos.
Regresión a la media
El fenómeno que acabamos de presenciar —no se predijo que los eventos extremos fueran tan extremos como resultaron ser— se relaciona directamente con la “regresión a la media”, un fenómeno estadístico para el cual ni siquiera necesitamos un pronóstico: Supongamos que observamos un serial temporal de ventas de un producto que no presenta estacionalidad ni ningún otro patrón dependiente del tiempo. Cuando, en un día determinado, las ventas observadas son mayores que las ventas promedio, podemos estar bastante seguros de que las observadas al día siguiente serán menores que las de hoy, y viceversa. Nuevamente, al seleccionar un valor muy grande o muy pequeño, debido a la naturaleza probabilística del proceso, es probable que seleccionemos una fluctuación aleatoria positiva o negativa, y las ventas eventualmente “regresarán a la media”. Psicológicamente, tendemos a atribuir causalmente esa regresión a la media —un fenómeno puramente estadístico— a alguna intervención activa.
Resolución: Agrupar por predicción, no por resultado. Mantener alerta ante posibles sesgos de selección.
¿Cuál es la solución a este dilema? Al agrupar por resultados, estamos seleccionando valores “bastante grandes” o “bastante pequeños” con respecto a su pronóstico; no estamos obteniendo una muestra representativa, sino una sesgada. Este sesgo de selección da lugar a grupos que contienen resultados que, naturalmente, están "bastante subestimados" o "bastante sobreestimados", respectivamente. Sufrimos del sesgo de selección retrospectivo si creemos que la predicción media y la observación media deberían ser iguales dentro de los elementos de movimiento “lento”, “medio” y “rápido”. Debemos convivir y aceptar la discrepancia entre las dos columnas. Por suerte, podemos emplear el teorema de Bayes para obtener el valor esperado realista. Una solución consiste, por tanto, en agregar otra columna a la tabla que contenga el valor teórico esperado de la predicción media por intervalo, que se puede comparar con la predicción media real en ese intervalo. Es decir, podemos cuantificar y reproducir teóricamente el sesgo de selección retrospectivo y comprobar si los datos agregados coinciden con la expectativa teórica.
Sin embargo, una solución mucho más sencilla consiste en formular preguntas diferentes a los datos, es decir, preguntas que estén alineadas con lo que nos promete el pronóstico. Esto nos permite comprobar directamente si estas promesas se cumplen o no: en lugar de agrupar por categorías de resultados, agrupamos por categorías de predicción, es decir, por predicciones de ventas lentas, medias y rápidas. Aquí podemos comprobar si se cumple la promesa del pronóstico (que las ventas medias dada una determinada predicción coincidan con esa predicción). Para nuestro ejemplo, obtenemos la siguiente tabla:
| Frecuencia de ventas prevista | ventas medias observadas | Predicción media |
| Lento <3 piezas/día | 1.288 | 1.267 |
| Medio 3 piezas/día | 5.247 | 5.229 |
| Rápido >3 piezas/día | 12.855 | 12.950 |
Teniendo en cuenta el número total de mediciones, una prueba de significación estadística sería negativa, es decir, no mostraría diferencias significativas entre la media de ventas observadas y la media de la predicción. Concluimos que nuestro pronóstico no solo es imparcial a nivel global, sino que también es imparcial por estrato de predicción.
En general, se puede evaluar un pronóstico filtrando según cualquier información que se conozca en el momento de la predicción, y el pronóstico debería ser imparcial en todas las pruebas. Sin embargo, el filtro no puede contener información futura, como las fluctuaciones aleatorias que ocurren en las observaciones, sobre las cuales la naturaleza decide solo en el futuro del punto de predicción en el tiempo.
¿Qué deberías aprender si llegaste hasta aquí? (1) Cuando se selecciona por resultado, no se tiene una muestra representativa. (2) Sea escéptico respecto de sus propias expectativas: las expectativas intuitivas que parecen muy razonables resultan ser erróneas. (3) Haga explícitas sus expectativas y pruébelas con casos bien conocidos.













