En la previsión de ventas minoristas, la cantidad de interés es la demanda de los clientes de un determinado producto, por ejemplo, cuántas cestas de fresas se aplicar. En la práctica, se observa una cantidad ligeramente pero significativamente diferente, a saber, las ventas registradas. Las ventas reflejan la demanda, pero están limitadas por la capacidad, es decir, por el nivel de existencias: cuando hay una demanda de 20 cestas, pero solo hay 12 disponibles, solo se venden 12 y no se satisface la demanda de los 8 clientes que también estaban dispuestos a comprar. La distinción entre ventas y demanda puede parecer una sutileza, pero esta entrada de blog le mostrará por qué confundir ventas con demanda conduce a capacitaciones sesgadas y evaluaciones de modelos defectuosas. Aprenderás cómo las existencias limitadas afectan a las ventas y cómo sortear los principales obstáculos para afrontar con confianza situaciones reales que impliquen existencias limitadas.
demanda y ventas
¿Cuál es la previsión más precisa que se te ocurra, una predicción de demanda infalible en la que puedas apostar sin dudarlo? En muchas situaciones, la respuesta es: ¡Simplemente pronostica “0” todo el tiempo! Ante una previsión de demanda nula, no se pedirá ni un solo artículo, no habrá artículos en los estantes, no se venderá ningún artículo. La predicción de cero ventas resultó ser totalmente acertada, coincidiendo perfectamente con las ventas nulas observadas. Esta predicción, absolutamente precisa, obviamente no es el pronóstico que hará feliz a tu jefe.
Este ejemplo extremo ilustra que hay que tener cuidado con lo que se pide: el objetivo de un minorista no es elaborar una previsión precisa, sino gestionar un negocio sostenible. La paradoja también pone de manifiesto un dilema fundamental en la previsión de la demanda: la propia previsión influye en el nivel de existencias que finalmente se proporciona, poniendo en peligro su evaluación. Podría argumentar que esta influencia existe por buenas razones, ¡para eso se hizo el pronóstico! Pero el nivel de existencias establece un límite máximo en la cantidad de artículos que se pueden vender, lo que restringe artificialmente los valores de ventas que se pueden observar. Esto genera una discrepancia entre la demanda hipotética (“cuánto se pide”) y las ventas observadas (“cuánto se vendió”). Las ventas observadas son la demanda real o las existencias disponibles, dependiendo de cuál sea menor.
En esta entrada de blog, les convenceré de que no hay forma de evitar un tratamiento probabilístico riguroso del problema de la demanda frente a las ventas. La distinción entre demanda y ventas, el tratamiento meticuloso de estas cantidades y de lo que predecimos y observamos con exactitud, es clave para el éxito y la correcta capacitación y evaluación de modelos.
Para que la idea sea tangible (y apetitosa), pensemos en un minorista que vende cestas de fresas frescas. El número entero de cestas vendidas puede entonces tratar como “piezas”. Lamentablemente, estos productos ultra frescos se desperdician cuando no se venden durante el día. Por lo tanto, realizar pedidos excesivos, es decir, tener más existencias de las que se aplicar, resulta costoso y debe evitar. Por otro lado, imagina que te apetece comprar fresas, pero cuando vas a buscarlas a tu supermercado habitual ya no hay: te conviertes en un cliente frustrado, cuya disposición a pagar no se materializó. Por lo tanto, realizar pedidos inferiores a los necesarios, es decir, tener menos existencias de las que se aplicar, también resulta costoso, tanto en términos de satisfacción del cliente como de pérdida de ingresos y beneficios.
Un minorista debe pedir la cantidad correcta de cestas de fresas para equilibrar cuidadosamente el desperdicio y las ventas perdidas. Por supuesto, para resolver este problema de pedidos, es necesario un pronóstico de demanda preciso que prediga realmente cuántas cestas se aplicar, y no cuántas se venden (recuerde la profecía autocumplida “0” mencionada anteriormente).
¿Cuánto venderemos?
Profundicemos un poco más en las previsiones de demanda y analicemos su significado. Un pronóstico de la demanda nos indica cuántos artículos se aplicar. Pero, ¿qué significa exactamente cuando “se aplicar 9,7 cestas”? Evidentemente, no se puede vender una cantidad fraccionaria de cestas de fresas; la interpretación literal es ridícula. Aun así, aceptamos y comprendemos intuitivamente el pronóstico, y lo interpretamos como una afirmación sobre el número medio esperado de cestas vendidas, el número de cestas que vendemos de media cuando la misma situación se repite muchas veces (y las existencias son siempre suficientes, lo que asumiremos por ahora). Por lo tanto, nuestro pronóstico oculta implícitamente alguna distribución de probabilidad, es decir, alguna concepción de qué tan probable es vender 1, 2, 3, … cestas, ya que solo indica el promedio de ventas esperadas. Se omite cuáles son esas probabilidades, o cuán cerca se encuentran las observaciones individuales (es decir, los números de ventas reales) alrededor de esa media de 9,7.
Levantemos la alfombra bajo la cual se ocultó la distribución de probabilidad para ver cómo debería ser. Emplearemos el siguiente gráfico para ilustrar nuestro ejemplo. A priori, las distribuciones de probabilidad con un valor esperado de 9,7 pueden adoptar formas muy diferentes: piense en una probabilidad del 51,5% de encontrar cero y una probabilidad del 48,5% de encontrar 20, como se muestra en el panel izquierdo. Esto da como resultado una media de 9,7 – aunque nunca se observa nada cercano a 9,7, como 9 o 10, sino solo valores extremos como 0 o 20. La distribución de probabilidad del panel central asigna una probabilidad del 70% a 10 y una probabilidad del 30% a 9; también tiene el valor esperado 9,7, pero la masa de probabilidad está mucho más concentrada entre los valores cercanos a la media, que por lo tanto se convierte en una buena estimación del número típico de ventas. El conjunto de distribuciones con una media de 9,7 es infinitamente grande, y la mayoría de esas distribuciones tendrán un comportamiento irregular (o “patológicas”, como les gusta decir a los matemáticos). Afortunadamente, podemos asumir distribuciones de probabilidad simples y bien comportadas, como la distribución de Poisson en el panel derecho (lea la publicación del blog "Pronosticar pocos es diferente" para saber por qué es una opción razonable).
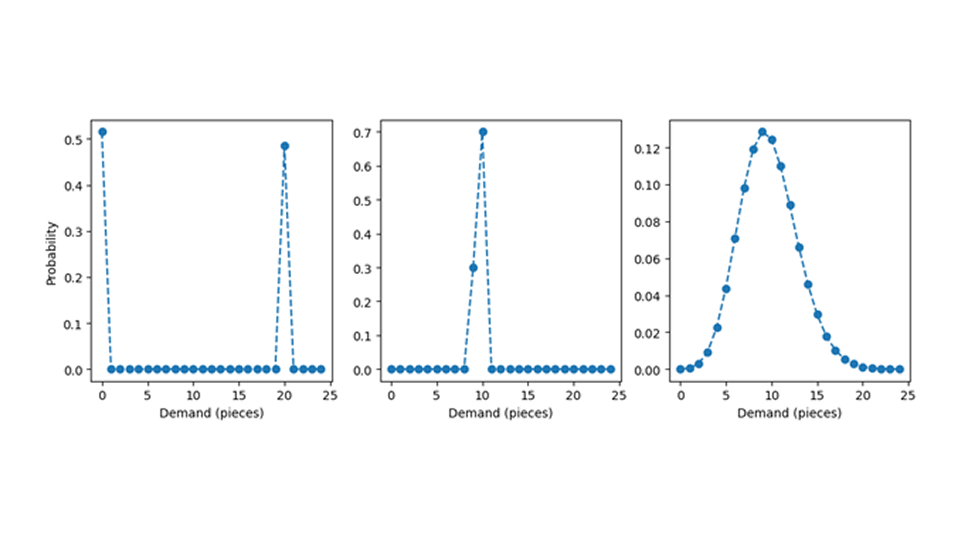
A lo largo de este texto, asumimos que el pronóstico produce la media de una distribución de Poisson prevista, y que la demanda realmente se distribuye según una distribución de Poisson, es decir, que el pronóstico es correcto. Incluso este escenario idealizado presenta suficientes complejidades como para justificar una entrada de blog.
Cómo las existencias finitas censuran la información
Demos ahora la bienvenida a la capacidad finita en este juego. Dada una distribución de la demanda, obtenemos la distribución de las ventas asignando a cada valor de demanda posible el valor de ventas resultante. Para todos los valores de demanda que sean inferiores o iguales al número de existencias disponibles, la demanda se traduce simplemente 1:1 en ventas: cuando hay 12 cestas disponibles, 5 cestas aplicar dan como resultado 5 vendidas, 12 cestas aplicar dan como resultado 12 vendidas. Cuando la demanda es mayor que las existencias, es decir, cuando la capacidad no es suficiente, las ventas están limitadas por el valor de las existencias: cuando se piden 13, 25 o 463 cestas, solo se venderán 12. Cuando se venden todas las existencias, hablamos de un evento de “golpe de capacidad”. Sin embargo, la masa de probabilidad asociada a la demanda de 13, 25 o 463 cestas debe “ir a algún sitio”, y efectivamente se suma a la probabilidad de que se aplicar las existencias totales. Las distribuciones de probabilidad de ventas para una demanda media de 9,7 y diferentes capacidades (16, 12, 8) se muestran en la siguiente figura.
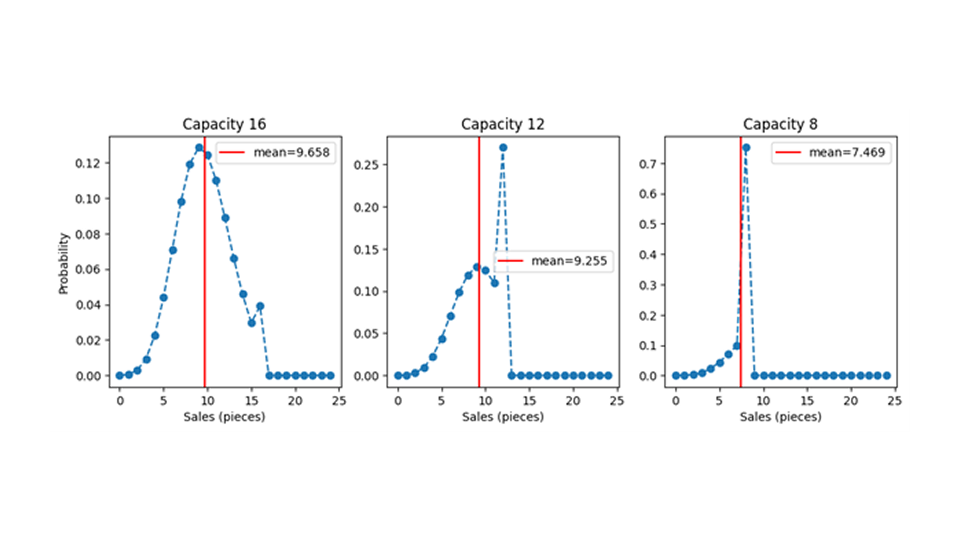
La capacidad finita censura la demanda de una manera que elimina información: cuando se establece una capacidad de 16 y se observa un impacto en la capacidad, es decir, 16 ventas, solo se puede inferir que la demanda fue al menos 16, no si fue 16, 25 o 7.624. La demanda real tiene un valor desconocido para usted – digamos, 47 – pero usted solo observa 16. Debido a la capacidad limitada, estamos perdiendo información de forma irrevocable (y no solo la satisfacción del cliente). Esta pérdida de información dificulta tanto el entrenamiento de modelos con capacidad finita como su evaluación.
Los gráficos también muestran las ventas medias esperadas como líneas rojas verticales. Quizás de forma sorprendente, la capacidad finita tiene un impacto en el valor esperado de las ventas incluso cuando la capacidad sigue siendo mayor que la demanda esperada. Es decir, si prevés una demanda de 9,7 y tienes 12 artículos en stock, ¡vendes de media menos de 9,7! ¡Necesitas almacenar más de lo previsto, en promedio, para vender exactamente lo previsto! Esto puede resultar confuso: para un evento individual, las ventas representan solo el mínimo entre la demanda y las existencias. Pero la media de la distribución de probabilidad de ventas no es necesariamente el mínimo entre la demanda esperada y la capacidad, ya que es necesario tener en cuenta la forma de la distribución de probabilidad. La razón de este comportamiento posiblemente sorprendente es que el valor de la demanda media prevista depende de fluctuaciones en torno a la media que, en promedio, se cancelan entre sí. Es decir, las fluctuaciones negativas (a veces se venden menos artículos que 9,7) se compensan con las positivas (a veces se venden más artículos que 9,7). Cuando la capacidad es finita, esas fluctuaciones positivas necesarias se suprimen y la cancelación de fluctuaciones positivas y negativas ya no se produce. Esto reduce la media de ventas prevista, incluso cuando la capacidad es mayor que la demanda media prevista.
El siguiente gráfico muestra las ventas esperadas en función de la capacidad, nuevamente para una demanda esperada de 9,7. Cuando la capacidad es mucho mayor que la demanda esperada (digamos, alrededor de 20), los eventos que se ven afectados por la capacidad finita son raros. En consecuencia, el número esperado de ventas permanece inalterado y cercano a 9,7. Cuando la capacidad es pequeña, digamos 5, entonces es casi inevitable que se alcance la capacidad y, en promedio, se venda un valor cercano a esa capacidad. Entre las 7 y las 14 aproximadamente, se produce una transición; la capacidad tiene un impacto fuerte, pero no totalmente determinante, en las ventas.
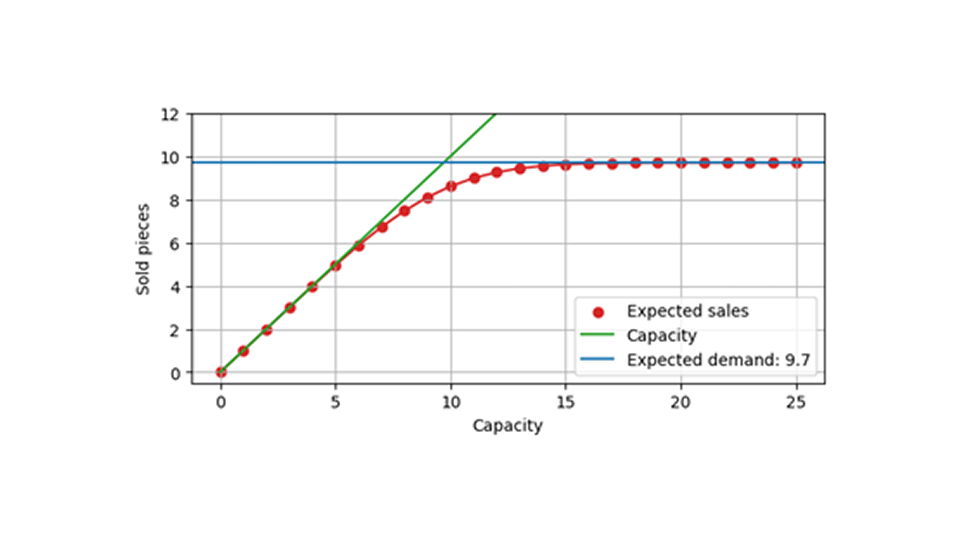
Entrenamiento y evaluación de modelos sobre demanda censurada
Ahora que tenemos bajo control nuestra herramienta principal —la distribución de probabilidad de las ventas, también conocida como distribución de demanda censurada por capacidad—, comprendamos qué debemos tener en cuenta al capacitar y evaluar modelos en tales circunstancias.
Necesitamos distinguir entre diferentes regímenes. Si se alcanzara la capacidad máxima todos los días, nunca se conocería la demanda real, sino solo un límite inferior de la misma ("vendimos 5 unidades, por lo que la demanda fue de al menos 5"). Afortunadamente, este es un escenario poco realista: cuando se alcanza la capacidad máxima todos los días, nos enfrentamos a muchos clientes insatisfechos y a mucha demanda insatisfecha; ningún minorista podrá mantener este modo de operar durante mucho tiempo. Si se ven obligados a hacerlo por restricciones de suministro, podrían considerar la posibilidad de modular la demanda aumentando los precios.
En el otro extremo, cuando nunca se alcanza la capacidad máxima, disfrutamos de un régimen ideal para hacer ciencia de datos: leemos la demanda real todos los días y, en esencia, podemos ignorar todas las discusiones sobre capacidad. Pero el sueño del científico de datos es la pesadilla del responsable de sostenibilidad: una enorme cantidad de residuos sería la consecuencia de tal estrategia de pedidos. Con una demanda prevista de 9,7, necesitaríamos mantener 21 artículos en stock para quedarnos sin existencias solo una vez cada 1.000 días.
Por lo tanto, normalmente se da una situación en la que a veces la demanda alcanza la capacidad (y el producto se agota en un momento dado del día), y otras veces no (y quedan algunas existencias por la noche). Esto es razonable, ya que es deseable un punto intermedio entre los objetivos contrapuestos de evitar el desperdicio y evitar la falta de existencias.
Debemos reconocer que construir el mejor modelo posible entra en conflicto con gestionar el mejor negocio posible: bajo una estrategia empresarial sostenible (cuando el desperdicio no es completamente “gratis”, pero se evita al menos en cierta medida), es inevitable que los productos se agoten en ocasiones. Sin embargo, la mejor ciencia de datos se realiza cuando se garantiza que nunca se producirán roturas de stock y cada valor de venta refleja directamente la demanda. Dado que realizamos ciencia de datos en un contexto empresarial, tendremos que convivir con el escenario intermedio y las ocasionales faltas de existencias.













